Mathematische Biologie
Biologische Systeme sind oft sehr kompliziert und dieser Umstand macht es schwer, Theorien aufzustellen, die ihr Verhalten erklären. Eine Möglichkeit, diese Schwierigkeit zu überwinden ist, mathematische Modelle zu verwenden. Ein mathematisches Modell für ein biologisches System ist ein mathematischer Konstrukt der wesentliche Aspekte der Biologie widerspiegelt obwohl er einfacher ist als das ursprüngliche System und deshalb leichter zu verstehen. Nachdem Einsichten über das Verhalten des Modells erreicht worden sind können sie übersetzt werden, um Einsichten über die Biologie zu erhalten.
Dynamische Systeme
In unserer Gruppe untersuchen wir die zeitliche Entwicklung von bestimmten biologischen Systemen. Die mathematischen Modelle, die diesen Zweck erfüllen sind dynamische Systeme. Es gibt verschiedene Varianten aber was sie gemeinsam haben ist, dass sie bestimmte Größen beschreiben, die von einer Variable abhängen, die die Zeit darstellt. Die Art von dynamischen Systemen auf die wir uns bisher hauptsächlich konzentriert haben sind gewöhnliche Differentialgleichungen. Im Allgemeinen hängen sie von bestimmten Parametern ab, z. B. Reaktionskonstanten. Das Ziel ist es, das qualitative Verhalten von Lösungen des Systems zu verstehen. Gibt es stationäre Zustände und wenn ja wie viele? Unter welchen Umständen konvergieren andere Lösungen gegen stationäre Zustände? Sind alle Lösungen beschränkt? Gibt es gedämpfte oder anhaltende Oszillationen?
Die Wahl der Modelle
In Modellen von biochemischen Systemen sind die Unbekannten die Konzentrationen von chemischen Stoffen. Sie nehmen an verschiedenen chemischen Reaktionen teil und bilden ein Reaktionsnetzwerk. Geeignete Annahmen über die Natur der Reaktionen (Kinetik) führen auf ein System von gewöhnlichen Differentialgleichungen. Es passiert oft, dass unterschiedliche mathematische Modelle für das gleiche biologische System aufgestellt werden. Dies führt zu Fragen der Beziehungen zwischen den verschiedenen Modellen und den Kriterien um zwischen ihnen zu wählen. In unserer Forschung gehen wir diese Fragen an. Welche Entscheidungen führen auf verschiedene Modelle? Das Ziel ist, eine Vereinfachung zu erreichen. Um dies zu tun verwerfen wir bestimmte Stoffe, die als zweitrangig betrachtet werden, und behalten andere. Ein solches Vorgehen ist notwendig, weil ansonsten die Anzahl der Unbekannten und Parameter im Modell so groß ist, dass ein Verständnis mit rein mathematischen Techniken oder mit Simulationen schwer zu erreichen wäre. Außerdem sind die vorhandenen experimentellen Daten zu den Mechanismen der Reaktionen begrenzt und man muss eine Wahl treffen, z. B. Massenwirkungs-Kinetik.
Maximale Vereinfachung (das 'low throughput'-Verfahren)
In der modernen Biologie sind Hochdurchsatz-Verfahren (englisch 'high throughput') sehr beliebt. Damit ist gemeint, dass man so viele experimentelle Daten wie möglich sammelt und so viele davon wie möglich in die Modelle einbaut. Es handelt sich im Prinzip dabei um mathematische Modelle aber letzten Endes spielen Computer-Simulationen die zentrale Rolle. Sie produzieren eine Art theoretische Daten. Diese Situation kann man als problematisch betrachten. Der Nobelpreisträger Sydney Brenner sagt 'We are drowning in a sea of data and thirsting for knowledge' [wir ertrinken in einem Meer aus Daten und dürsten nach Wissen]. Im einem alternativen Verfahren, das man als 'low throughput' bezeichnen könnte, versuchen wir das System so weit wie möglich zu reduzieren, während wesentliche Eigenschaften erhalten bleiben. Im Detail können wir an einen Prozess in drei Schritten denken. Im ersten Schritt ersetzen wir ein 'großes' Modell durch eine 'kleines'. Im zweiten Schritt analysieren wir das kleine Modelle so detailliert wie möglich. Im dritten Schritt untersuchen wir in wie fern die Schlüsse, die wir für das kleine Modell erhalten haben sich auf das große erweitern lassen. In der Tat kommt dieser Prozess in drei Schritten zwischen den anderen zwei Schritten wo das Modell ausgehend von der Biologie produziert wird und wo die mathematische Ergebnisse benutzt werden um biologische Schlüsse zu erlauben.
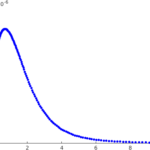
Beispiel 1. Aktivierung von T-Zellen
T-Zellen sind weiße Blutkörperchen, die zwischen fremden und körpereigenen Stoffen innerhalb des Organismus unterscheiden sollen und das Immunsystem entsprechend lenken sollen. Wie gut sie dieses Ziel erreichen beeinflusst Infektionskrankheiten, Autoimmunkrankheiten und Krebs. Wir untersuchen das Anfangsstadium der Aktivierung von T-Zellen, die ersten drei Minuten. Ein Modell für diesen Prozess wurde von Grégoire Altan-Bonnet und Ron Germain eingeführt. Es handelt sich um ein 'großes' Modell, mit mehr als 250 Unbekannten. Später haben Paul François und Kollegen eine viel einfachere Alternative eingeführt. Zusammen mit Eduardo Sontag (damals an der Rutgers University) haben wir das Modell von François et al. mathematisch untersucht. Wir konnten auch die Eigenschaften von Lösungen dieses Modells direkt mit Fragen von biologischem Interesse in Verbindung bringen. Kann es z. B. passieren, dass unter bestimmten Bedingungen ein Stoff der eine T-Zelle stärker stimuliert zu einer schwächeren Antwort führt? Wenn ja kann dieses Phänomen auf Vorgängen basieren die während des Anfangsstadiums passieren und deshalb durch das Modell von François et al. beschrieben werden? Wir haben eine positive Antwort auf diese Fragen erhalten. Das Modell von Altan-Bonnet und Germain wird im Promotionsprojekt von Pia Brechmann weiter untersucht.
(mit E. D. Sontag) Multiple steady states and the form of response functions to antigen in a model for the initiation of T cell activation. R. Soc. open sci. 2017 4 170821. Preprint version.
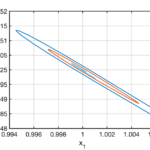
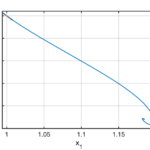
Beispiel 2. Steuerung der Aktivität der Kinase Lck
Die Immun-Checkpoint-Therapie ist ein vielversprechender neuer Ansatz im Kampf gegen Krebs, bei dem Antikörper benutzt werden, um die Angriffe von T-Zellen auf Tumore zu verstärken. Momentan verwenden die erfolgreichsten Therapien dieser Art den Stoff PD-1. Die Mechanismen, durch die PD-1 T-Zellen stimuliert werden, sind leider noch nicht gut verstanden. Mathematische Modelle könnten etwas dazu beitragen, die Situation zu verbessern. In einem schon vorhandenen Modell dieser Art spielt der Stoff Lck eine zentrale Rolle. Mit dieser Motivation haben Lisa Kreusser (damals an der University of Cambridge, UK) und ich angefangen, Modelle für die Kontrolle der Aktivität von Lck zu untersuchen. Lck katalysiert seine eigene Phosphorylierung und dies kann zu einer komplexen Dynamik führen. Wir haben bewiesen, dass ein einfaches Modell für Lck Oszillationen aufweist.
(mit L.M. Kreusser) Autophosphorylation and the dynamics of the activation of Lck. Bull. Math. Biol. 83, 64 (2021). Preprint version.

Beispiel 3. Der Calvin-Zyklus der Photosynthese
Der Calvin-Zyklus ist ein Teil der Photosynthese. Es gibt viele mathematische Modelle dieses Systems und wir haben ihre Eigenschaften und ihre Beziehungen untereinander untersucht. Vor kurzem, im Rahmen des Promotionsprojekts von Hussein Obeid, haben wir den Fall eines maximal vereinfachten Systems untersucht, das von Brian Hahn eingeführt wurde. Es ist zweidimensional und wir konnten es in großem Detail untersuchen. Beschränkte Lösungen konvergieren immer gegen stationäre Zustände, aber es gibt auch unbeschränkte Lösungen, die in Abwesenheit der Photorespiration auftreten. Damit hatten wir eine mathematische Bestätigung der Idee von Hahn, dass die Photorespiration den Calvin-Zyklus stabilisieren kann. Diese Ergebnisse sind in einer Zeitschrift erschienen. In der Doktorarbeit, die aus diesem Projekt entstanden ist, wurden einige der schon veröffentlichten Ergebnisse auf andere komplizierte Modelle der Dimension drei erweitert. Insbesondere konnte gezeigt werden, dass es in diesen Systemen keine Oszillationen gibt, was mathematisch aufwendig war. Dabei hat die Theorie der monotonen dynamischen Systeme eine zentrale Rolle gespielt.
(mit H. Obeid) The minimal model of Hahn for the Calvin cycle. Math. Biosci. Eng. 16, 2353-2370 (2019) Preprint version.
Beispiel 4. Ein Modell des Calvin-Zyklus mit Diffusion
Vor einigen Jahren haben Juan Velazquez und ich einige Aspekte der Dynamik zweier grundlegender Modelle des Calvin-Zyklus untersucht. Folgende biologisch motivierte Frage blieb damals offen: Wenn dieses Modell so modifiziert wird, dass die Diffusion von ATP berücksichtigt wird (so dass das System gewöhnlicher Differentialgleichungen in ein System von Reaktion-Diffusion-Gleichungen verwandelt wird) entstehen dadurch zusätzliche stationäre Lösungen? Vor kurzem haben Burcu Gürbüz und ich eine Arbeit geschrieben, in der wir eine positive Antwort auf diese Frage liefern. In der Tat gibt es unendlich viele inhomogene stationäre Lösungen für gegebene Werte der Parameter. Wir haben auch bewiesen, dass alle diese stationären Lösungen instabil sind, womit sie die Rolle nicht spielen können, die in der ursprünglichen Motivation vorgesehen war.
(mit B. Gürbüz) Analysis of a model of the Calvin cycle with diffusion of ATP. Preprint.
(mit J. J. L. Velázquez) Dynamical properties of models for the Calvin cycle. J. Dyn. Diff. Eq. 26, 673-705 (2014). Preprint version.
Beispiel 5. Modelle für Hepatitis B und C
Zusammen mit Kollegen aus Kamerun haben wir Modelle für die Dynamik von Infektionskrankheiten in einem Wirt untersucht. Mit der Gruppe von Calvin Tadmon (Dschang) haben wir ein Modell für Hepatitis B untersucht, das die Diffusion von Virionen und Verzögerungseffekte berücksichtigt. Es beinhaltet auch die Auswirkung der humoralen Immunität. Wir haben die Existenz und Stabilität von stationären Lösungen untersucht. Mit der Gruppe von Alexis Nangue (Maroua) haben wir ein Modell für Hepatitis C untersucht, das durch gewöhnliche Differentialgleichungen definiert wird. Es beinhaltet eine Beschreibung der Replikation von RNA, die für dieses Virus spezifisch ist. Wir haben die Existenz und Stabilität von stationären Lösungen untersucht und einige Ergebnisse über die Konvergenz von allgemeineren Lösungen gegen stationäre Lösungen erhalten. Ein wichtiger Aspekt dieser Argumente ist die Verwendung einer Methode von Li und Muldowney.
(mit A. Nangue, B. Kammegne Tcheugam, und P. S. Kamdem Simo) Analysis of an initial value problem for an extracellular and intracellular model of hepatitis C virus infection. Preprint.
(mit S. Foko und C. Tadmon) Global stability analysis of a delay cell-population model of hepatitis B infection with humoral immune response. Dyn. Sys. 36, 537-559 (2021).
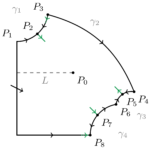
Beispiel 6. Das Selkov-Modell der Glykolyse
Die Glykolyse ist der Prozess durch den lebende Organismen Energie aus Zucker erhalten. In bestimmten Fällen kann eine konstante Eingangskonzentration zu einer oszillierenden Ausgangskonzentration führen. Ein wesentlicher Schritt im Prozess, der die Quelle der Oszillationen ist, wurde von Evgeny Selkov modelliert. Er hat ein zweidimensionales Modell mit Massenwirkungs-Kinetik aufgeschrieben. Dieses Modell hat Pia Brechmann in ihrer Masterarbeit untersucht und wir haben einige Ergebnisse dieser Arbeit zusammen mit einigen Erweiterungen veröffentlicht. Die Theoreme liefern ein ziemlich vollständiges Bild der Dynamik des Systems. Insbesondere gibt es unbeschränkte Lösungen für alle Werte der Parameter. In dieser Arbeit ist eine Frage unbeantwortet geblieben. Ist es so, wie Selkov behauptet hat, dass es Lösungen gibt, die auf eine oszillatorische Weise unbeschränkt werden, d.h. kann eine Bahn wie eine Spirale aussehen, die unbegrenzt expandiert? In einem weiteren Artikel haben wir bewiesen, dass Lösungen dieser Art tatsächlich existieren und haben untersucht, was in einem anderen Modell passiert, das auch von Selkov betrachtet wurde und wo Massenwirkung durch Michaelis-Menten-Kinetik ersetzt wird.
(mit P. Brechmann) Unbounded solutions of models for glycolysis. J. Math. Biol 82, 1 (2021). Preprint version.
(mit P. Brechmann) Dynamics of the Selkov oscillator. Math. Biosci. 306, 152-159 (2018). Preprint version.
Beispiel 7. Phosphorylierungssysteme
In biologischen Systemen werden Informationen oft in den Phosphorylierungszuständen verschiedener Proteine gespeichert. Ein relativ einfaches Beispiel ist der mehrfache vergebliche Zyklus, wo ein Protein an mehreren Stellen auf eine Weise phosphoryliert werden kann, die bestimmte Regeln erfüllt. Liming Wang und Eduardo Sontag bewiesen, dass die Anzahl der stationären Zustände über alle Grenzen mit der Anzahl der Phosphorylierungsstellen wächst. Was noch fehlte war eine strenge und optimale untere Schranke für die Anzahl der stationären Zustände und ein Beweis der Stabilitätseigenschaften dieser Zustände. Mit Juliette Hell haben wir gezeigt, dass im Fall von zwei Phosphorylierungsstellen die optimale untere Schranke für die Anzahl der stabilen stationären Zustände gleich zwei ist. Neulich haben Elisenda Feliu, Carsten Wiuf und ich dieses Ergebnis auf den Fall beliebig vieler Phosphorylierungsstellen verallgemeinert.
(mit E. Feliu und C. Wiuf) A proof of unlimited multistability for phosphorylation cycles. Nonlinearity 33, 5629–5658 (2020). Preprint version.
(mit J. Hell) A proof of bistability for the dual futile cycle. Nonlin. Analysis: RWA. 24, 175-189 (2015). Preprint version.